Es llevar los resultados a cuadros para facilitar
su proceso y es llevar los cuadros a gráfico para hacer las primeras
interpretaciones. Cada pregunta lleva
asociado un cuadro y una gráfica, y para relacionar una o más variables
se pueden hacer un cruce de variable o tabla de contingencia.
1. Tabulación
para variables cualitativas.
Se
lleva la información o un cuadro así: Significado de cada variable
n= Tamaño de la muestra
xi=
Se llama variable de interés
ni= Se llama frecuencia absoluta. Es elnúmero de veces que se repite cadaopción
de la variable de interés.
hi= Se llama frecuencia relativa, contiene elporcentaje de participación de cada una
delas opciones de la variable de interés. Y sehalla por la formula
hi= nin*100%.
2.
Tabulación tipo II, frecuencia o en forma compuesta.
Se
utiliza para la variable discreta llevando la información en un cuadro a significado
de cada variable
n= Tamaño
de la muestra
xi= variable
de interés contiene los diferentes resultados de la variable
discreta. Se coloca de menor a mayor. Y aunque este se repita se
coloca una solo vez
Ni = Frecuencia absoluta acumulada contiene el número
de veces que se repite la variable de
interés desde la primera hasta la respectiva esto quiere decir que
va acumulando la absoluta
Hi=Frecuencia
relativa acumulada. Lleva la frecuencia absoluta acumulada a porcentaje se
puede hallar de dos formas.
Medidas estadísticas
Las medidas estadísticas tienen
la importancia de dar a conocer algunos aspectos de la población, en cuanto a
la cantidad y calidad de los valores de
los elementos de ella.
Las medidas estadísticas se clasifican en:
·
MEDIDAS ESTADÍSTICAS DE POSICIÓN.
(ubicadas entre los valores extremos
de la variable analizada).
·
MEDIDAS ESTADÍSTICAS DE DISPERSIÓN.
(denominadas también de abarcamiento, generalmente alrededor de la media
aritmética )
Fórmulas para las medidas estadísticas de Posición ( D.N.C.).
Def. Sean x1 , x2 , x3 ,............., xn-1 , xn, n
valores obtenidos por una variable X en una población P.
Se definen las medidas estadísticas de posición como sigue:
Mediana.
Es el valor de la variable que deja la mitad (50%) a la derecha y la
otra mitad (50%) a la izquierda.
Para calcular el valor de la mediana primeramente deben ordenarse de
menor a mayor, o viceversa, todos los n elementos de la población. Una vez
ordenados se aplica uno de los siguientes criterios:
10 EJEMPLOS DE TABULACIÓN Y GRÁFICAS DE DATOS
Distribución de frecuencias: muestra el número de veces que
ocurre cada observación.
Ejemplo: Se elaboró una encuesta en
un jardín de niños y ésta informó que las mascotas más comunes que tiene un
niño son perros,
gatos, peces,
hámsteres y pájaros
|
perro
|
gato
|
perro
|
hamster
|
|
pájaro
|
hamster
|
gato
|
perro
|
|
hámster
|
gato
|
pájaro
|
gato
|
|
perro
|
perro
|
hámster
|
pájaro
|
|
perro
|
perro
|
pájaro
|
gato
|
A continuación se muestra la distribución de
frecuencias absolutas, relativas y porcentuales de las mascotas mas comunes de
los niños.
|
Mascota
|
Frecuencia absoluta
|
Frecuencia relativa
|
Frecuencia acumulada
|
|
Perro
|
7
|
.35
|
35 %
|
|
Pajaro
|
4
|
.20
|
20 %
|
|
Hamster
|
4
|
.20
|
20 %
|
|
gato
|
5
|
.25
|
25 %
|
Estos datos se pueden representar en una gráfica de barras o en una
gráfica de pastel:
Gráfica de barras
Gráfica de pastel
Ejemplo de tablas estadísticas:
AUTOBUSES FORANEOS
1) Toma
de datos
Los
siguientes datos corresponden a la cantidad de asientos vacíos que reportaron
50 autobuses foráneos en un domingo.
|
12
|
11
|
4
|
6
|
6
|
11
|
3
|
10
|
12
|
4
|
|
10
|
1
|
1
|
2
|
4
|
5
|
2
|
4
|
4
|
8
|
|
8
|
7
|
8
|
4
|
10
|
4
|
2
|
6
|
2
|
9
|
|
5
|
6
|
6
|
4
|
12
|
8
|
1
|
12
|
1
|
7
|
|
7
|
6
|
8
|
4
|
6
|
9
|
3
|
7
|
7
|
5
|
2)
Ordenación de datos
|
1
|
2
|
4
|
4
|
5
|
6
|
7
|
8
|
9
|
11
|
|
1
|
2
|
4
|
4
|
5
|
6
|
7
|
8
|
10
|
12
|
|
1
|
2
|
4
|
4
|
6
|
6
|
7
|
8
|
10
|
12
|
|
1
|
3
|
4
|
4
|
6
|
6
|
7
|
8
|
10
|
12
|
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
11
|
12
|
Rango = 12-1 = 11
3) Tamaño
de clase
No de
clases = 1 + 3.332log (50) = 6
Tamaño de
clase = 11/6 = 2
4) Límites de
clase
5)
Límites reales de clase
6) Marca
de clase
|
Clase
|
Intervalo
|
LRI
|
LRS
|
Frec.
Absoluta
|
Frec.
Relat
|
Frec.
Porcentual
|
X
|
|
|
LI
|
LS
|
|||||||
|
1
|
1
|
2.9
|
0.95
|
2.95
|
8
|
.16
|
16 %
|
1.95
|
|
2
|
3
|
4.9
|
2.95
|
4.95
|
11
|
.22
|
22 %
|
3.95
|
|
3
|
5
|
6.9
|
4.95
|
6.95
|
10
|
.20
|
20 %
|
5.95
|
|
4
|
7
|
8.9
|
6.95
|
8.95
|
10
|
.20
|
20 %
|
7.95
|
|
5
|
9
|
10.9
|
8.95
|
10.95
|
5
|
.10
|
10 %
|
9.95
|
|
6
|
11
|
12.9
|
10.95
|
12.95
|
6
|
.12
|
12 %
|
11.95
|
|
total
|
50
|
1
|
100 %
|
|||||
Representación
gráfica de datos.
Se tomará
el ejemplo anterior para demostrar el uso de diferentes gráficas.
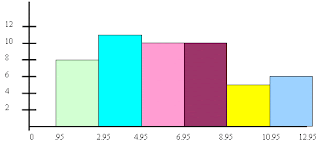
Histograma: forma gráfica de barras que
emplea variables con escala de
intervalos o de proporciones. Para realizarla, se toma en cuenta para el eje X,
los Límites reales, y para el eje Y, las frecuencias absolutas.
Polígono
de frecuencias: Forma
gráfica que representa una distribución de frecuncias en la forma de una línea
continua que traza un histograma. Para su elaboración, se consideran las marcas de
clase en el eje X y las frecuencias absolutas en el eje Y.
Gráfica
de barras: la
gráfica de barras es una forma de gráfica que utiliza barras para indicar la
frecuencia de ocurrencia de las observaciones. Para construirla se constituye
el eje y por las frecuencias absolutas y el eje X por los límites inferior y
superior de cada clase, dejando un espacio entre barra y barra.
MAS EJEMPLOS
ALUMNO: HERNÁNDEZ CUEVAS JORGE ALBERTO
GRUPO: 533
COBAO PL- 04 "EL TULE"







.jpg)








No hay comentarios:
Publicar un comentario